En todos los intentos realizados hasta nuestros días para demostrar que 2+2 = 4, nunca se ha tenido en cuenta la velocidad del viento. La suma de números enteros no es en efecto posible más que con un tiempo bastante tranquilo para que, una vez puesto el primer 2, se quede en su sitio hasta que se pueda poner la pequeña cruz, después el segundo 2, y después el pequeño muro en el que sentarse para reflexionar y por fin el resultado. El viento puede soplar después, y dos y dos son cuatro. Pero ¿Qué pasaría si el viento empieza a ser más fuerte? Visto en Matemáticas en la Biblioteca, de Marta Macho Stadler (UPV/EHU)

Pues nos encontraríamos el primer número caido. Y si sigue soplando fuerte, también el segundo. ¿Cuál sería entonces el resultado de  ? Las matemáticas actuales no están en la medida de respondernos.

Si el viento sopla fuerte, entonces la primera cifra sale volando, después la crucecita, y así sucesivamente. Pero supongamos que disminuye tras la desaparición de la cruz, entonces podríamos estar abocados a escribir la absurdidad 2 = 4.

El viento no sólo lleva, también trae. La unidad, número particularmente ligero y que una simple brisa puede desplazar, puede caer en una suma donde no tiene nada que hacer, a espaldas incluso del calculador. Esta es la intuición que tuvo el matemático ruso Dostoievski cuando osó declarar que tenía una debilidad por 2 + 2 = 5.

Las reglas de la numeración decimal prueban del mismo modo que probablemente los hindús debieron formularse más o menos inconscientemente nuestro axioma. El cero rueda con facilidad, es sensible al mínimo soplido. Tampoco se le tiene en cuenta cuando está situado a la izquierda de un número: 02 = 2, ya que el cero se larga siempre antes del final de la operación. No es significativo más que a la derecha, pues entonces las cifras precedentes pueden también retenerlo e impedirle salir volando. También se tiene 20 ≠ 2, mientras el viento no supere algunos metros por segundo.

Deduciremos ahora algunas consecuencias prácticas de estas consideraciones; en cuanto se teme que haya perturbaciones atmosféricas, es bueno dar a la suma una forma aerodinámica. Está también aconsejado escribir de derecha a izquierda y comenzar lo más cerca posible del borde de la hoja de papel. Si el viento hace deslizar la operación en curso se puede, casi siempre, recogerla antes de que llegue al margen. Se obtendrá así, aún con una tormenta de equinoccio, resultados como éste: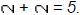 

Fuentes:

• Matemáticas en la Biblioteca (Diapositiva 107), de Marta Macho Stadler (UPV/EHU).
• 2(tumbado) más 2(tumbado) son cinco, en ::ZTFNews.org
• Quelques remarques sommaires relatives aux propriétés aérodynamiques de l'addition es un cuento escrito y publicado por Raymond Queneau en 1950. Se incluyó más adelante en Contes et propos (Gallimard, 1981).