"Repetir es persuadir con más detalle".
Figura 1.- Geometría fractal del romanescu.
Esta cita célebre, atribuida al Duque de Levis, puede darnos una idea del concepto de fractal. ¿Alguna vez has entrado en un supermercado, y en la sección de verduras has comprobado asombrado la intrigante forma que adoptan los romanescus, primos raros de las coles, el brócoli o la coliflor? ¿No resulta increíble pensar en la asombrosa geometría, repetida por toda su superficie, hasta formas infinitas?
¿Qué es un fractal? La respuesta no es sencilla, pero podemos simplificar la idea asumiendo que se trata de objetos cuya estructura básica se repite a escalas infinitas, de forma total o parcial. Este concepto fue desarrollado por el matemático polaco Benoît Mandelbrot en los años 70. Lejos de ser artificios, los fractales pueden encontrarse de forma común en la naturaleza, como ocurre con los romanescus, siendo más cotidianos de lo que cabría imaginar. Algunos ejemplos pueden observarse en las siguientes fotografías:
Figura 2.- Ejemplos de fractales en la naturaleza. A) Concha con geometría fractal. B) Daucus carota. C) Los rayos también presentan geometría fractal.
Quizás lo más curioso de los fractales sea su dimensión fraccionaria, ya que si los observamos a cualquier escala, se reconoce una estructura muy alejada de los objetos unidimensionales, bidimensionales o tridimensionales, como suele ser habitual.
La construcción de fractales puede realizarse de manera sencilla mediante experimentos como los realizados por Sierpinski o Koch, como se muestra en las siguientes imágenes:
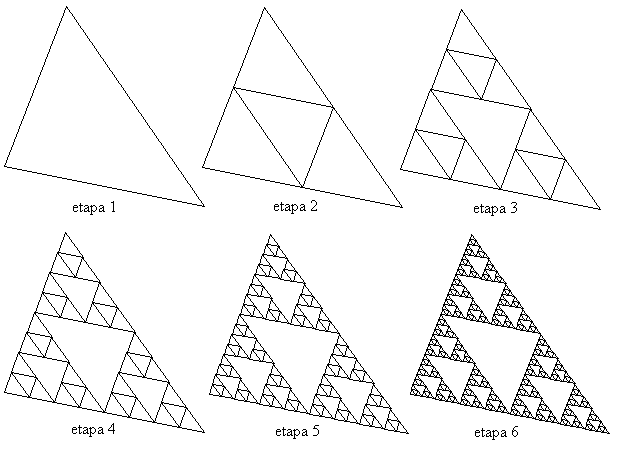

Figura 3.- A) Etapas en la construcción del fractal de Sierpinski. B) Etapas en la construcción del fractal de Koch.
Los fractales no se encuentran únicamente en la naturaleza como tal, sino que cuentan con múltiples aplicaciones en compresión de datos o imágenes, en la modelización de algunos procesos biológicos o incluso en la producción de piezas musicales.
Para aprender
Leer las matemáticas
Uno de los mejores libros que puede adentrar a los más pequeños al mundo de las Matemáticas es el escrito por Hans Magnus Enzensberger, titulado "El diablo de los números", en los que Robert, un joven al que no le gustan demasiado el mundo de las matemáticas, comienza a tener sueños extraños por las noches, en los que se le aparece el Diablo de los números, quien le empieza a explicar con sencillos ejemplos a Robert curiosidades como los números primos o la serie de Fibonacci.
 Reseña
Reseña
H.M. Enzensberger: "El diablo de los números". Editorial Siruela, Madrid, 1ª edición, 1998.
ISBN: 9788478444335
Figura 4.- Portada del libro.







