EL PAÍS, de la mano de la Real Sociedad Matemática Española y como en años anteriores, recupera este verano su sección de retos matemáticos. Se publicará cada jueves hasta final de agosto un problema y se invitará a los lectores a resolverlo antes de las 00.00 del martes siguiente. Ese día se da el nombre del ganador, que se eligirá por sorteo de entre los acertantes y que obtendrá como premio la colección de libros Grandes Ideas de la Ciencia. El primer desafío lo presenta Adolfo Quirós, viejo conocido de los aficionados a esta sección, impulsor de los desafíos, profesor de la Universidad Autónoma de Madrid y vicepresidente de la Real Sociedad Matemática Española. Las soluciones deberán enviarse al correo electrónico desafiodeagosto1@gmail.com antes de las 00.00 del martes 5 de agosto (medianoche del lunes al martes). Para considerar como válida una respuesta no basta con que la solución sea la correcta, hay que explicar cómo se ha llegado a ella.

Primer reto: Números a la parrilla

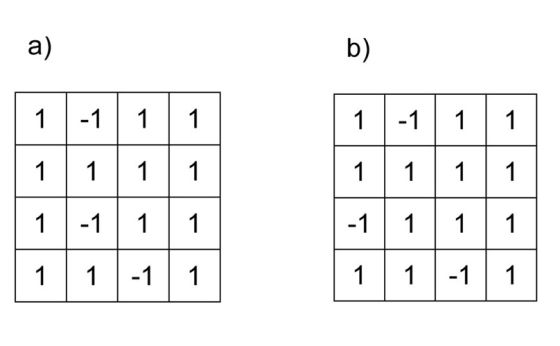
Empezamos con una parrilla 4x4 que en cada casilla tiene un 1 o un -1. El juego consiste en cambiar los valores de algunas casillas, siguiendo las reglas que se darán, y se gana si se consigue que haya un 1 en todas las casillas.

Se puede jugar con dos reglamentos distintos:

-Reglamento ACB (el más estricto): se pueden cambiar simultáneamente los valores de todas las casillas de una fila, de una columna, o de una de las dos diagonales.

-Reglamento NBA (más laxo): además de los movimientos autorizados por las reglas ACB, son también válidos los movimientos que consisten en cambiar simultáneamente los valores de todas las casillas de una recta paralela a una de las dos diagonales, incluido cambiar sólo el valor de una esquina.

Consideramos dos situaciones iniciales que pueden verse en esta figura

Para cada una de ellas nos preguntamos si se puede ganar, y cómo, con cada una de los reglamentos. Así que el desafío es cuádruple: para cada una de las dos posiciones iniciales, y con cada uno de los dos reglamentos, dar la cadena de movimientos que permite ganar la partida o demostrar por qué no se puede.

Otros retos anteriores

----------------------------------------------------------------------------------------------------------------------------------

NOTA A LOS LECTORES: Con este post 2+2=5 se despide hasta el mes de septiembre. Los retos matemáticos así como los los retos de ingenio publicados ayer se podrán seguir en El País. ¡Felices vacaciones!